
이전글에서 bm25공식을 분석해보았으니 이번에는 한번 직접 공식을 구현해보겠습니다.
숫자 가지고놀기 좋은 파이썬으로 한 번 짜보겠습니다. 네이밍이나 변수명은 elastic의 것을 따라했습니다.
from math import log
def idf(docFreq, docCount):
return log(1 + (docCount - docFreq + 0.5) / (docFreq + 0.5))
def tfNorm(termFreq, avgFieldLength, fieldLength, k1=1.2, b=0.75):
return (termFreq * (k1 + 1)) / (termFreq + k1 * (1 - b + b * fieldLength / avgFieldLength))
def bm25(docFreq=18, docCount=7857, termFreq=3, avgFieldLength=364.4447, fieldLength=113.7778, k1=1.2, b=0.75):
return idf(docFreq, docCount) * tfNorm(termFreq, avgFieldLength, fieldLength, k1=k1, b=b)
bm25()
>>> 11.153388335189215
bm25 function에는 저번 포스팅에서 결과로 떨어진 값들을 default로 지정해놔서 argument를 따로 안줘도 내가 원하는 특정값의 변경만 확인 가능하게 했습니다.
이제 이 function들을 만든 이유인 값을 내가 직접 변경해보면서 score가 어떤 방향으로 변하는지를 확인 해보도록 하겠습니다.
만일 문서에서 검색이 1번 적중했을때와 10번 적중했을때 스코어가 어떤식으로 달라지는지 한 번 봐보도록 합시다. python의 for generator 패턴을 사용하면 매우 쉽게 이런 작업을 수행할 수 있습니다.
scores = list(bm25(termFreq=x) for x in range(1, 11))
>>> scores
[8.42096347631024, 10.316515470029008, 11.153388335189215, 11.624892352130258, 11.927428051730507, 12.138021241868652, 12.293056096265454, 12.411956398132178, 12.5060366172696]
결과가 잘 뽑히긴 했는데 확실히 어떤 상황인지 잘 모르겠네요. 차트로 한 번 그려보도록하겠습니다. python의 matplotlib을 쓰면 매우 쉽게 차트를 그릴 수 있습니다.
import matplotlib.pyplot as plt
plt.plot(scores, label='termFreq')
plt.legend(loc='lower right')
plt.show()
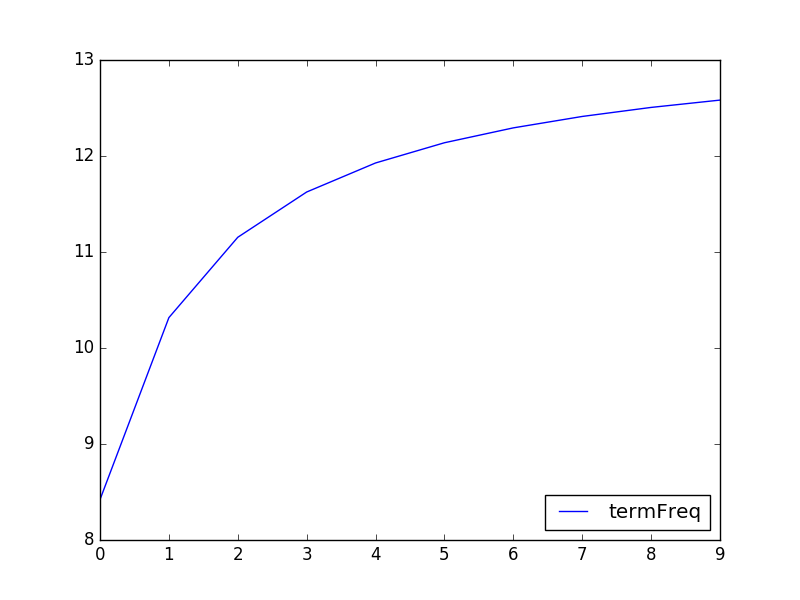
아까 숫자만 봤을때보다 훨씬 눈에 들어오네요! 한가지 알 수 있는건 term적중이 1,2,3,4처럼 순차적으로 증가해도 실제 스코어는 완만한 곡선을 그리며 증가한다는 것을 알 수 있습니다. 곡선을 그린다는 것은 더 유연한 스코어를 만들며 스코어에 limit가 생긴다는 뜻이 됩니다.
term frequency에 주어졌던 가중치 k1을 변경하면 어떻게 될까요? k1을 2로 변경하고 다시 테스트 해보겠습니다.
scores = list(bm25(termFreq=x, k1=2.) for x in range(1, 11))
plt.plot(scores, label='termFreq k1=2')
plt.legend(loc='lower right')
plt.show()
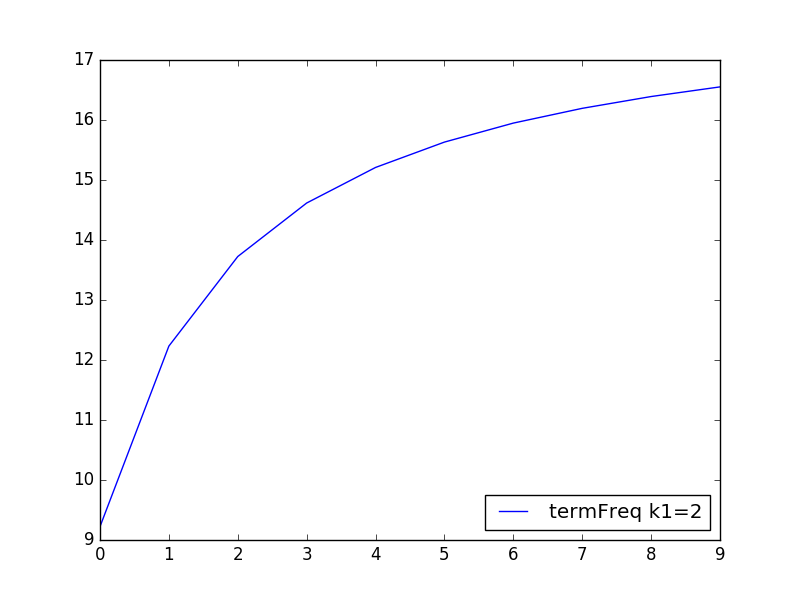
곡선의 기울기는 큰 변화가 없으나 점수의 min수치과 max수치의 편차가 좀 더 벌어진것을 알 수 있습니다. 즉 term frequency로 좀 더 큰 점수 변동폭을 주고 싶으면 k1수치를 올리면 될 것 같습니다.
scores = list(bm25(termFreq=x, b=1.25) for x in range(1, 11))
plt.plot(scores, label='termFreq b=1.25')
plt.legend(loc='lower right')
plt.show()
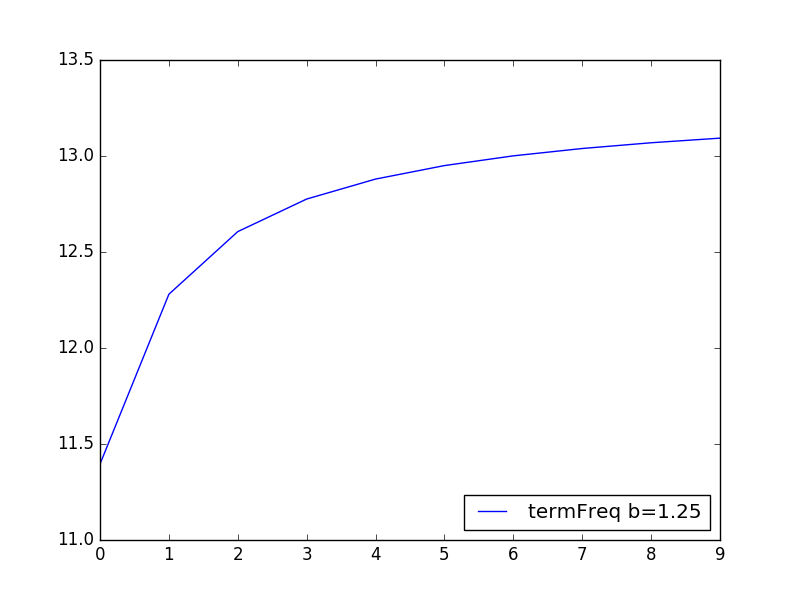
b의 0.75를 1.25로 조절해봤습니다. 이전 그래프랑 비슷한데 자세히 보면 곡선이 조금 완만 해진것을 확인 가능하고 스코어도 비율이 좀 좁아진것을 확인 가능합니다.
scores = list(bm25(termFreq=x, b=1.5) for x in range(1, 11))
plt.plot(scores, label='termFreq b=1.5')
plt.legend(loc='lower right')
plt.show()
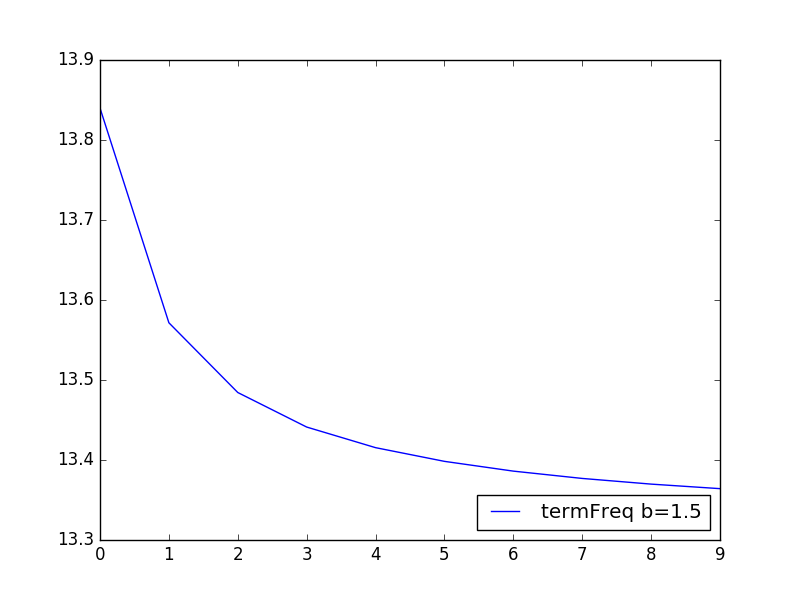
그리고 1.5로 설정하면 점수가 뒤집어집니다. 어…음??
이번엔 IDF를 테스트 해보겠습니다. doc Frequency를 높여보면서 수치를 봐보겠습니다.
docCount = 7857 # 저번에 테스트해본 doc count는 7857개였다.
docFreqs = [int(docCount / 50. * x) for x in range(1, 51)]
>>> docFreqs
[157, 314, 471, 628, 785, 942, 1099, 1257, 1414, 1571, 1728, 1885, 2042, 2199, 2357, 2514, 2671, 2828, 2985, 3142, 3299, 3457, 3614, 3771, 3928, 4085, 4242, 4399, 4557, 4714, 4871, 5028, 5185, 5342, 5499, 5657, 5814, 5971, 6128, 6285, 6442, 6599, 6757, 6914, 7071, 7228, 7385, 7542, 7699, 7856]
scores = [bm25(docFreq=(df)) for df in docFreqs]
plt.plot(docFreqs, scores, label='docFreq')
plt.legend(loc='upper right')
plt.show()
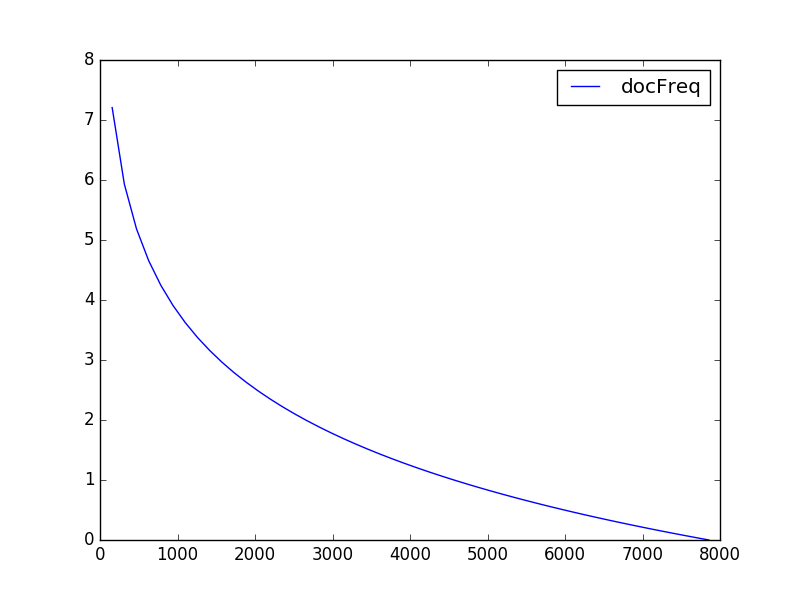
저번 포스팅에 얘기 했었던 문서마다 많이 등장하는 term일수록 스코어가 낮아진다라는 공식과 일치하는것을 확인하실 수 있습니다. 특히 전체 문서개수와 거의 동일한 수준으로 가면 tf가 점수가 있다 하더라도 0점에 가깝게 떨어지는것을 알 수 있습니다.
필드 길이도 어느정도 영향을 미치는지 한 번 확인해보죠. 평균 필드길이를 500으로 놓고 100부터 1000까지 필드길이를 변화했을때 스코어를 봐보겠습니다.
fieldLengths = [x * 100 for x in range(1, 11)]
scores = [bm25(fieldLength=fl, avgFieldLength=500) for fl in fieldLengths]
plt.plot(fieldLengths, scores, label='fieldLength')
plt.legend(loc='upper right')
plt.show()
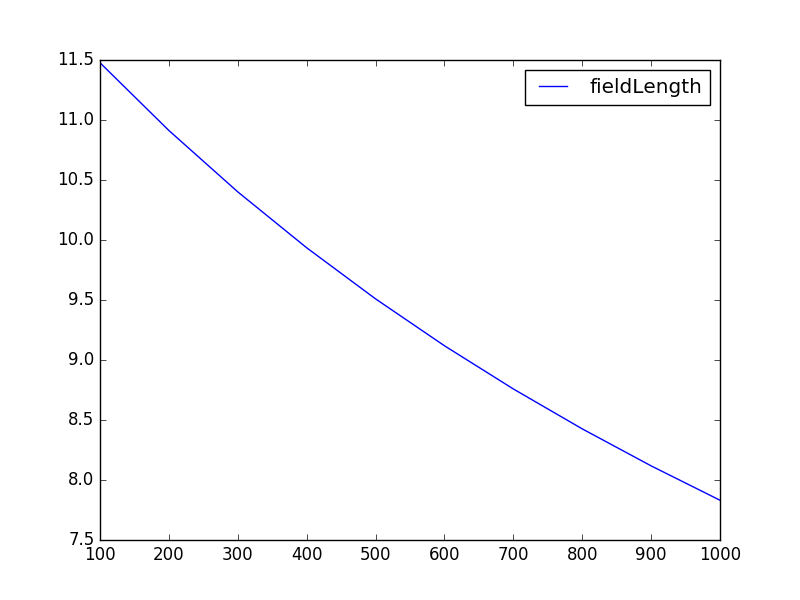
적중된 필드의 길이가 적을수록 점수가 높고 필드 길이가 길수록 점수가 낮아지는것을 확인 할 수 있습니다. 그리고 다른 조건들에 비해 경사가 거의 일직선인것을 확인 가능합니다.
python을 사용하면 쉽게 이런 공식들을 적은량의 코드로 쉽게 확인이 가능합니다. 공식만 보고 그냥 그런가보다 하고 넘어가는 것보다 직접 이렇게 차트로 그려보면 그 데이터의 성질과 수치변화시 발생하는 현상등을 쉽게 관찰이 가능하네요.
국내에 검색엔진 관련된 문서가 많지 않아 이런쪽을 더 포스팅 해보고 싶네요. 그럼 안뇽!